Három érdekesség (másképp)

1.) Cipő­fű­zés másképp
Már lát­tam régeb­ben is (talán Gabá­nál?), de most megint elő­jött. Szó­val cipő­fű­ző meg­kö­té­se, annyi a csa­var, hogy a végén nem így, hanem úgy viszed a fűzőt. Ered­mény: nem olyan könnyen lazu­ló cso­mó. Ma kipró­bál­tam, álta­lá­ban a szimp­la cso­mó két órát bír a Lacos­te-on, most dél­után 5‑ig tartott.

2.) Szor­zás másképp
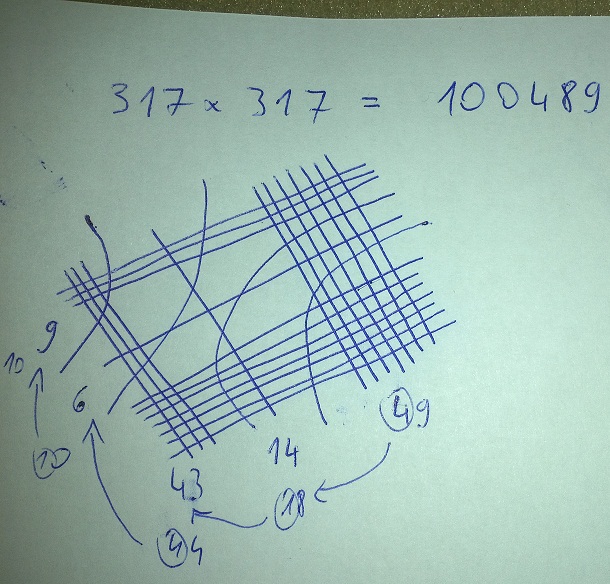
Lóci osz­tot­ta meg face­book-on, és nagyon meg­tet­szett. Gya­kor­la­ti hasz­na kb. nul­la, de ennyi­re vic­ces mate­ma­ti­kai dolog­gal rég nem talál­koz­tam. Nyil­ván kipró­bál­tam két három­je­gyű szám­mal, kifo­gyott a tin­ta a tol­lam­ból, mire végig­vo­nal­káz­tam, de kijött :)

3.) Négy­zet­re eme­lés másképp
A fen­ti FB-poszt­hoz kom­men­tel­te Bon­cók Dániel:

Végy egy szá­mot (pl. 42, mert ugye…):
Ebből a szám­ból vonj ki 25-öt és az ered­ményt szo­rozd fel 100-al ([42–25]x100=17x100=1700)
Illet­ve ezt a szá­mot vond ki 50-ből, az ered­ményt emeld négy­zet­re ([50–42]^2=8^2=64)
A két ered­ményt össze­ad­va meg­ka­pod a válasz­tott szám négyzetét:
1700+64=1764
42x42=1764

És tény­leg. A hát­tér­ben per­sze egy igen egy­sze­rű magya­rá­zat van, miszerint
(A — 25) x 100 = 100A — 2500
és
(50 — A)^2 = 2500 — 100A + A^2
Össze­ad­va, átrendezve:
100A — 2500 + 2500 — 100A + A^2 = 100A — 100A — 2500 + 2500 + A^2 = A^2

Ennek, ha lehet, még keve­sebb gya­kor­la­ti hasz­na van, talán 50 köze­li szá­mok­nál jön jól, ha nincs nálad szá­mo­ló­gép, tele­fon vagy toll-papír. Pl. a 49 négy­ze­te (49 — 25) x 100 = 2400 és (50 — 49)^2 = 1 össze­ge, azaz 2401.